이진탐색트리
이진 탐색 트리는 다음과 같은 속성이 있는 이진 트리 자료 구조이다.
- 각 노드에 값이 있다.
- 값들은 전순서가 있다.
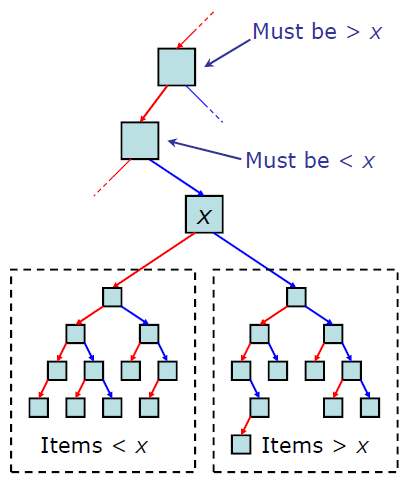
- 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.
즉, 이진 트리 구조로 되어있는데 자식의 왼쪽 값이 부모보다 작고 오른쪽 값이 부모보다 크면 이진탐색트리다.
이진탐색 트리를 순회 할 때는 중위 순회 방식(왼쪽-루트-오른쪽)을 쓴다. 이렇게 하면 이진탐색트리 내에 있는 모든 값들을 정렬 된 순서로 읽을 수 있다.

예시로, 다음의 이진탐색 트리를 중위 순회하면 1, 3, 5, 7, 8, 10으로 정렬된 형태다.
탐색

아래 이진탐색트리에서 10을 탐색한다고 가정하자.
이진탐색트리는 부모노드가 왼쪽 자식노드보다 크거나 같고, 오른쪽 자식노드보다 작거나 같다는 점에서 시작하여 탐색을 진행한다.
우선 루트노드(7)와 10을 비교합니다. 10은 7보다 크므로 왼쪽 서브트리(1, 3, 5)는 이제 고려할 필요가 없다. 탐색공간이 대폭 줄어든다는 얘기입니다. 이러한 방법을 특정 노드를 찾을 때까지 계속해서 반복한다.
이진탐색트리의 탐색 연산에 소요되는 계산복잡성은 트리의 높이(루트노드-잎새노드에 이르는 엣지 수의 최대값)가 h일 때 O(h)가 된다.
삽입
앞서 탐색 예시로 든 트리에 4를 삽입한다고 가정해보자.

이진탐색트리의 속성이 깨지지 않아야 하기 때문에 삽입 연산은 반드시 리프 노드에서만 이루어진다. 현재 숫자보다 크면 오른쪽,작으면 왼쪽으로 자식으로 내려가다가 자식이 없는 지점을 만났을 때, 삽입을 진행한다.
이진탐색트리 삽입 연산의 시간 복잡도는 삽입할 위치의 잎새노드까지 찾아 내려가는 데 h번 비교를 해야 하기 때문에 O(h)가 된다. 노드 삽입 자체는 O(1)이라 무시할만한 수준이다.
삭제
1) 자식 노드가 없는 경우 : 삭제할 노드를 그냥 없애기만 하면 된다.
2) 자식 노드가 하나 있는 경우 : 해당 노드를 지우고, 해당 노드의 자식노드와 부모노드를 연결해준다.

이진탐색트리의 속성 때문에 20을 루트노드로 하는 서브트리의 모든 값은 20의 부모노드인 30보다 작거나 같다.
따라서 20을 지우고, 20의 하나뿐인 자식노드(25)와 부모노드(30)를 연결해도 이진탐색트리의 속성이 깨지지 않는 걸 확인할 수 있습니다.
3) 자식 노드가 2개인 경우 :

이진탐색트리 구조상 successor(삭제 대상 노드의 오른쪽 서브트리의 최소값)는 자식노드가 하나이거나, 하나도 존재하지 않는다. 각각 살펴보면 다음과 같습니다.
- successor의 자식노드가 하나인 케이스 : 위 예시 그림과 같습니다. 삭제 대상 노드의 오른쪽 서브트리가 30을 루트노드로 하는 트리일 때, 이 트리의 맨 왼쪽 노드인 20은 하나의 자식노드(25)를 갖습니다.
- successor의 자식노드가 존재하지 않는 케이스 : 삭제 대상 노드의 오른쪽 서브트리가 아래 그림과 같을 때에는 successor는 자식노드를 가지지 않습니다.
-

그래서 이 케이스에서의 삭제 과정은
- 삭제 대상 노드의 오른쪽 서브트리를 찾는다.
- successor(1에서 찾은 서브트리의 최소값) 노드를 찾는다.
- 2에서 찾은 successor의 값을 삭제 대상 노드에 복사한다.
- successor 노드를 삭제한다.
로 진행할 수 있다.
이진 탐색 트리의 한계점
이진탐색트리 핵심 연산인 탐색, 삽입, 삭제의 계산복잡성은 모두 O(h)다. 그러나 트리가 다음과 같은 경우 문제가 된다.

극단적으로는 n개의 노드가 크기 순으로 일렬로 늘어뜨려져 높이 또한 n이 되는 경우도 이진트리탐색에 해당한다. 이 경우에서 결과적으로 이진탐색트리의 계산복잡성은 O(n)이라는 얘기다.
이러한 경우는 탐색 속도가 O(logn)으로 빠른 이진탐색을 계승했다고 보기 어렵다. 이 때문에 트리의 입력, 삭제 단계에 트리 전체의 균형을 맞추는 이진탐색트리의 일종인 AVL Tree가 제안되었다.
AVL트리
AVL트리는 다음과 같은 특징을 가진다.
- 이진 탐색 트리의 속성을 가진다.
- 왼쪽 오른쪽 서브 트리의 높이 차가 최대 1이다.
- 높이 차가 1보다 커지면 회전을 통해 균형을 맞춰 높이 차를 줄인다.
- 삽입, 검색, 삭제의 시간 복잡도가 O(logN)이다.
AVL트리는 Balance Factor를 이용하여 그래프의 균형이 무너졌는지 아닌지를 판단한다.
이는 BF(K) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이로 구할 수 있다.

AVL트리는 모든 노드의 BF가 -1,0,1 중 하나여야 한다. 만약 이를 벗어나면 균형이 깨졌다는 것을 의미하고, 이때 회전이 필요한 것이다.
AVL 트리의 회전
AVL 트리에서 삽입 삭제가 일어날 때 노드들의 배열에 따라 4가지(LL, RR, LR, RL) 불균형이 발생할 수 있으며 각 상황마다 rotation에 방향을 달리하여 트리의 균형을 맞춘다.
LL(Left Left) case
y는 z의 왼쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우 right rotation을 수행한다.

- y노드의 오른쪽 자식 노드를 z노드로 변경한다.
- z노드 왼쪽 자식 노드를 y노드 오른쪽 서브트리(T2)로 변경한다.
- y는 새로운 루트 노드가 된다.
RR(Right Right) case
y는 z의 오른쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left rotation을 수행하여 균형을 맞춘다.

- y노드의 왼쪽 자식 노드를 z노드로 변경합니다.
- z노드 오른쪽 자식 노드를 y노드 왼쪽 서브트리(T2)로 변경합니다.
- y는 새로운 루트 노드가 됩니다.
LR(Left Right) case
y는 z의 왼쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left , right 순으로 총 두 번의 rotation을 수행하여 균형을 맞춘다.

RL(Right Left) case
y는 z의 오른쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우, right, left 순으로 총 두번의 rotation을 수행하여 균형을 맞춘다.

'Computer Science > 알고리즘, 자료구조' 카테고리의 다른 글
| Heap과 Priority Queue (0) | 2023.04.03 |
|---|---|
| 탐색 알고리즘 (0) | 2023.04.01 |
| Hashing과 Hash Table (0) | 2023.04.01 |
| 그래프와 탐색 (0) | 2023.04.01 |
| 시간 복잡도 (0) | 2023.03.31 |



